Submitted by ve10 on
1TG0 is an evil protein. At least that is my latest assessment of version 5.0’s attempts at folding it. I think of proteins as puzzles and, just like sudoku, the term evil is reserved for the very trickiest variety. An evil protein commands my respect.
Now that code development has settled down, I’ve begun doing some systematic studies on various proteins. The second protein attempted, 1AHO, like 2P5K folded quite easily and gave a great RMSD value of 4.4Å. But things turned out differently with the third protein, 1TG0.
Unlike the first two proteins, 1TG0 has no alpha-helices at all. It’s mostly comprised of long strands that occasionally align beta-sheet-like. That already makes it trickier. Whereas the alpha-helices in a fold can assemble independently, there needs to be a lot of coordination among beta strands for them to assemble into sheets (or in this case “ribbons” because 1TG0 is small).
The scatter plot below summarizes the results of 14 attempts to fold 1TG0. One of the points, colored green, doesn’t count because I started the algorithm on the native fold. For all the others I used different random starts. Everything else about the 14 experiments was the same, in particular, the non-native litemotif file for the backbone constraints (for 1TG0 I had an average of 199 litemotifs per 4-sequence). To allow for the possibility that not all of 1TG0’s litemotifs have counterparts in other proteins, I set the number of litemotif constraints that may be ignored at a hopeful six.
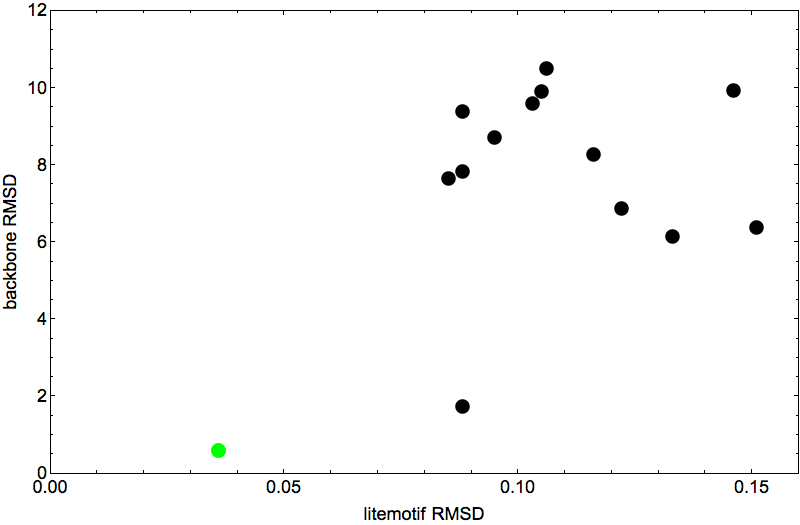
Shown on the horizontal axis is the final constraint discrepancy achieved by the folding algorithm. This number can approach zero only when we include native litemotifs among the constraints. Here, because native litemotifs are removed, the discrepancy runs into a “noise floor”. These small numbers are root-mean-square distances (in angstroms) for the 4+1 atom groups in an average litemotif. Usually many of the litemotifs are much closer than this number, and so the average is dominated by a smaller number of outliers. The six most extreme outliers (which go unconstrained) are not included in this average.
The final discrepancy values are so close to what I consider to be the noise floor, that it seems unlikely that the algorithm would have produced lower discrepancies had I let it run longer. My termination criterion was that after reaching discrepancy 0.15Å, the algorithm should make another 104 iterations before outputting the fold.
The vertical axis of the scatter plot gives the RMSD comparison of the output of the folding algorithm and the native fold (after alignment). It is the lack of a clear relationship, between these vertical values and the horizontal discrepancies, that makes 1TG0 so evil. That’s because the discrepancy is the only evidence we have on how well the folding algorithm is doing, and the plot shows that this does a poor job at identifying the best fold (vertical axis). The two native/fold comparisons below put this in chilling perspective:
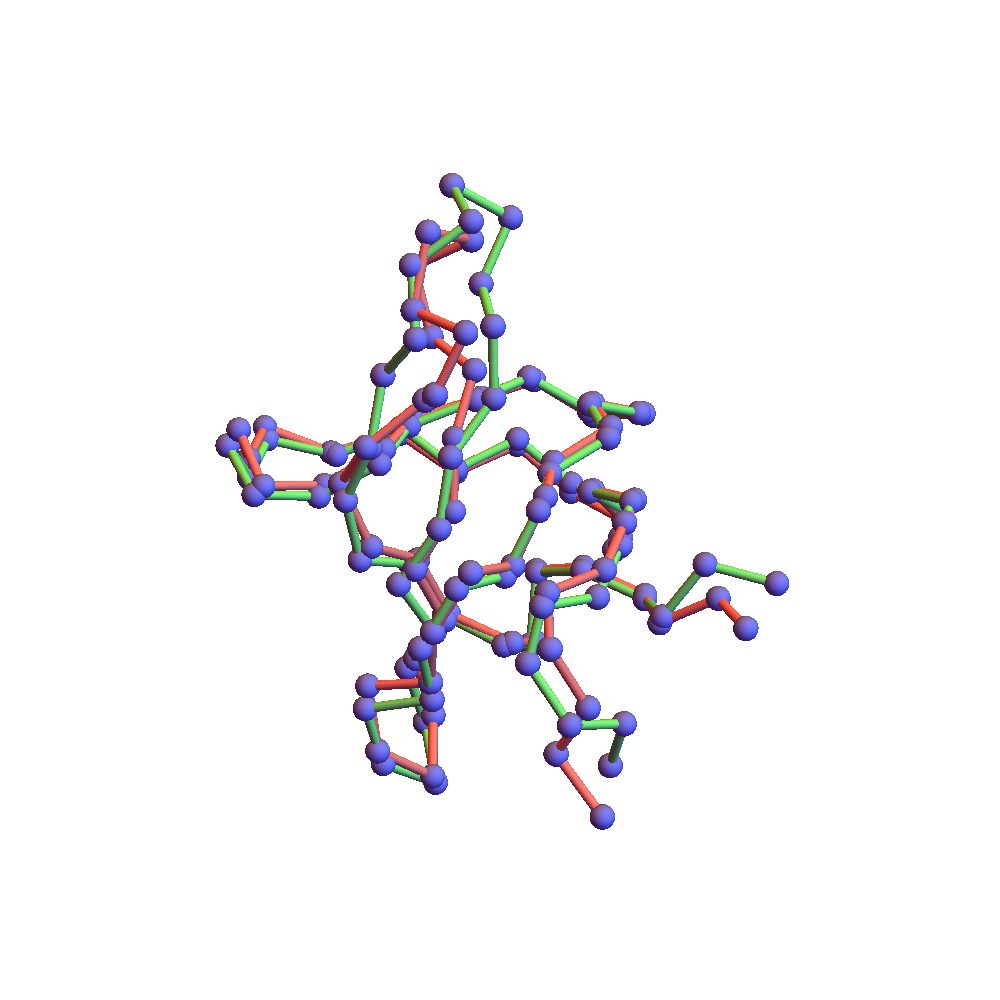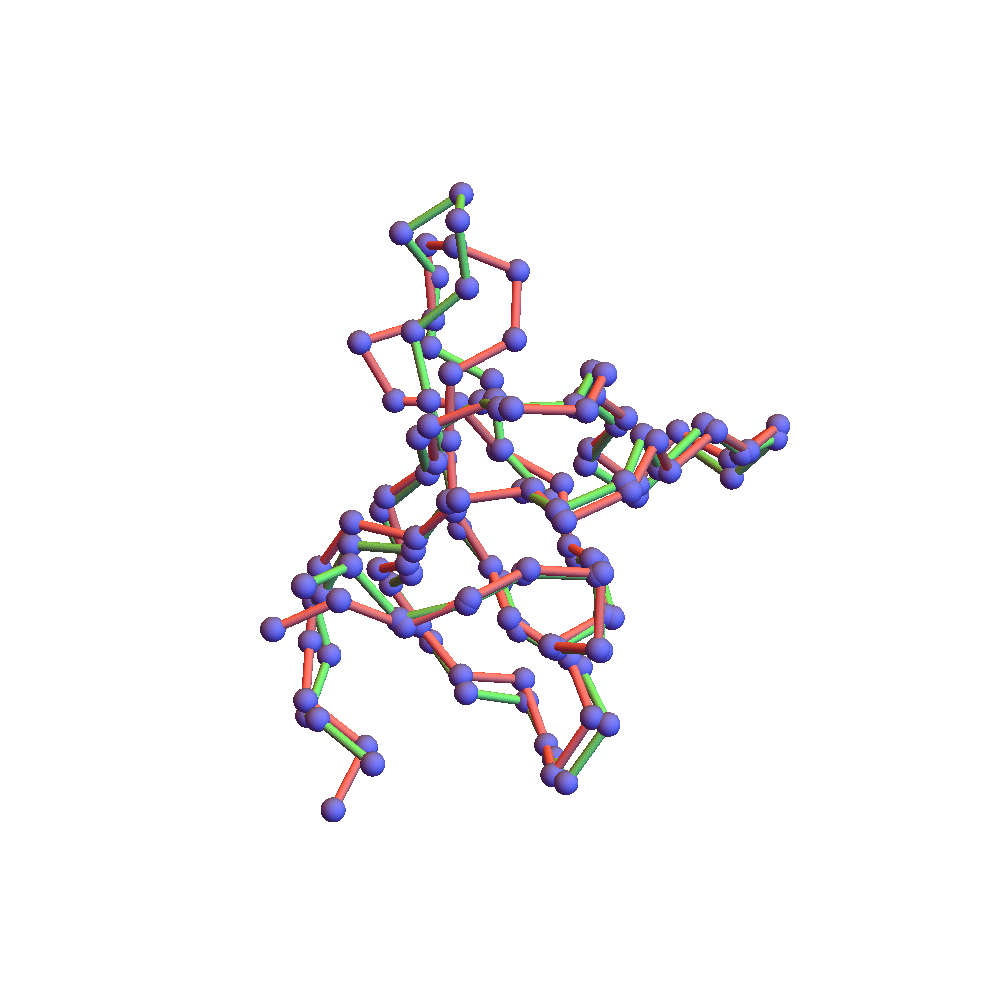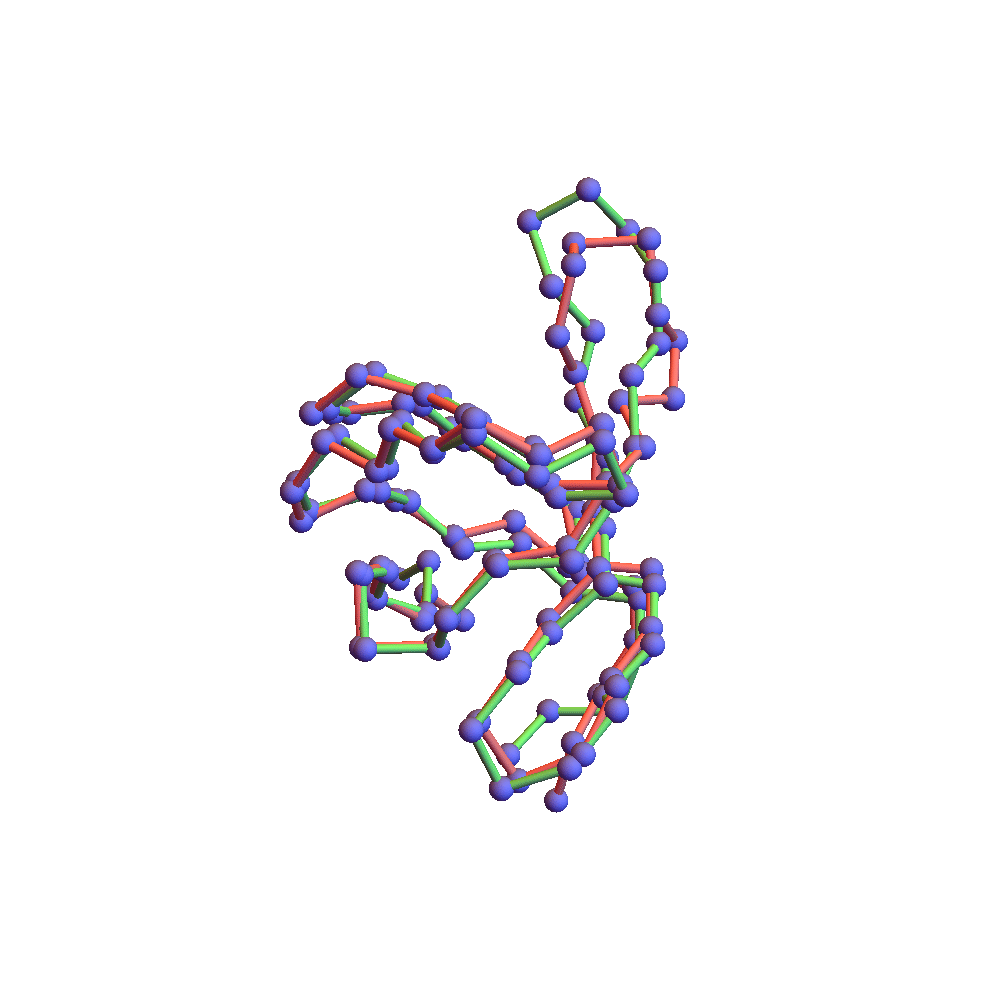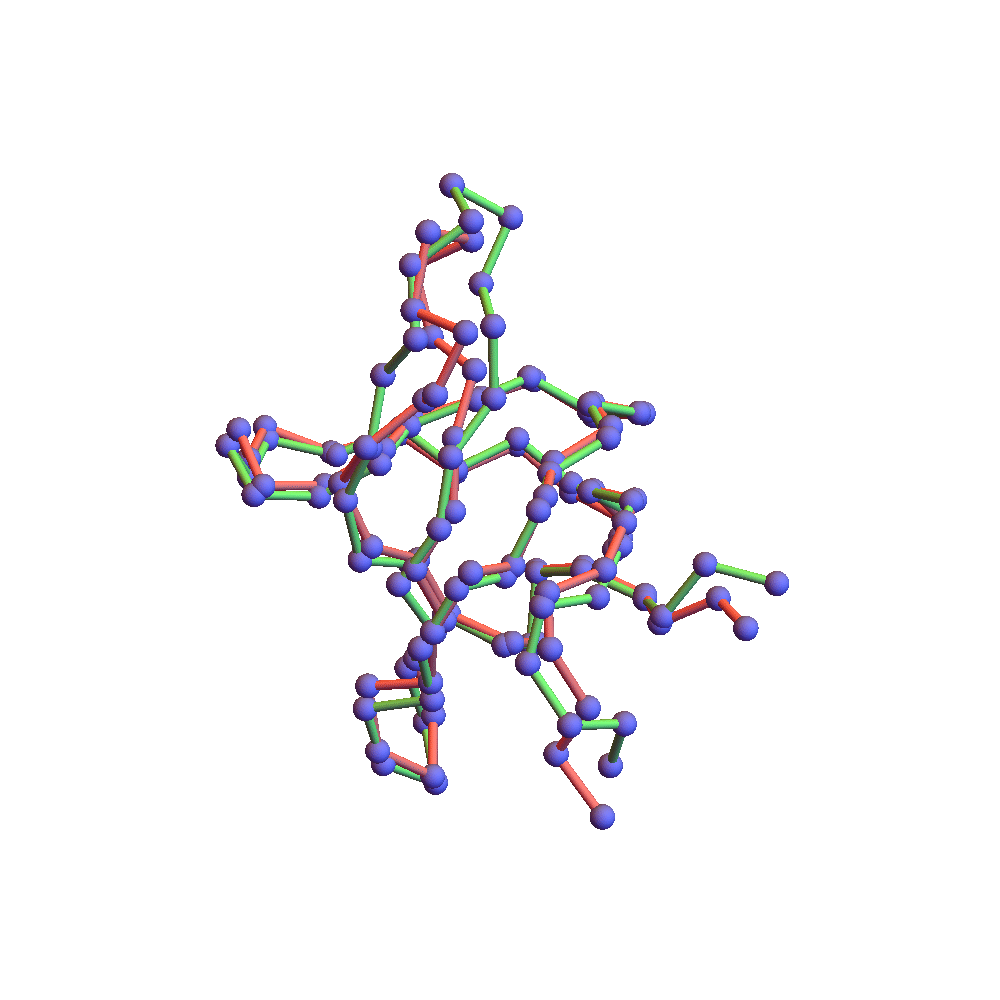
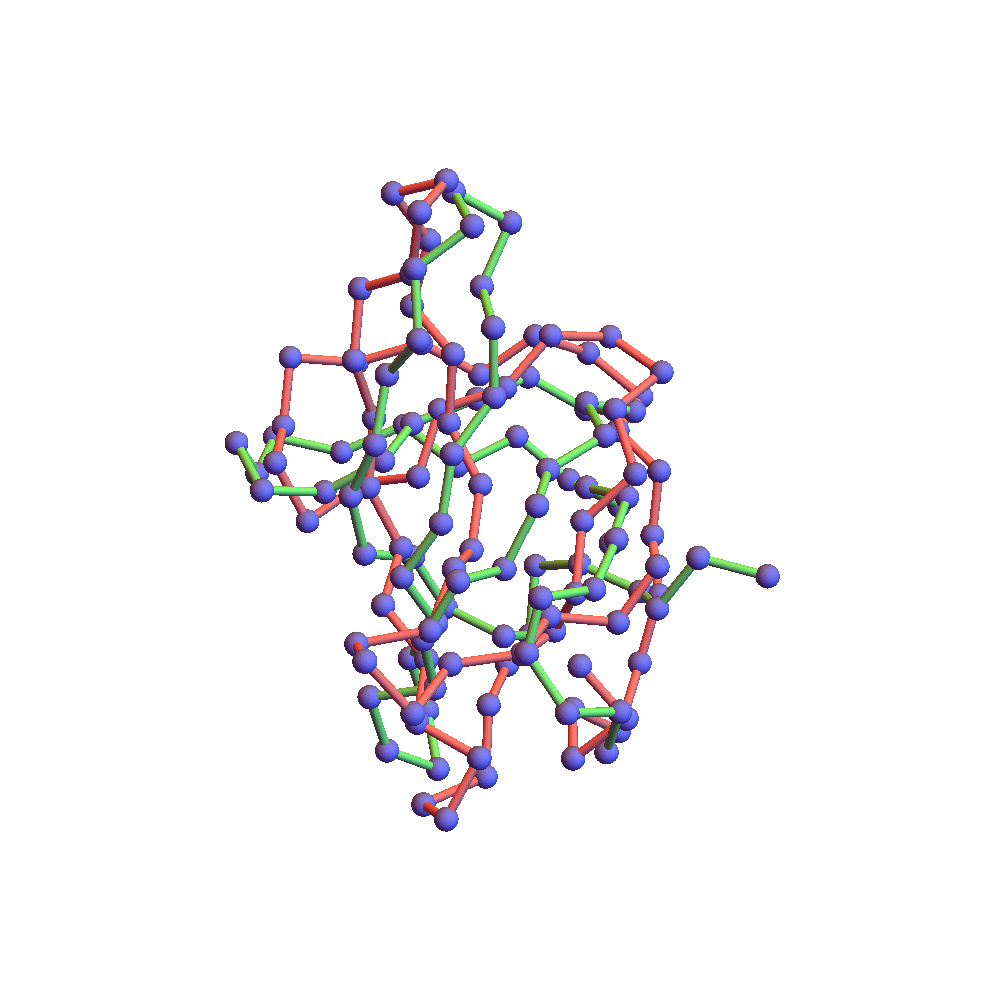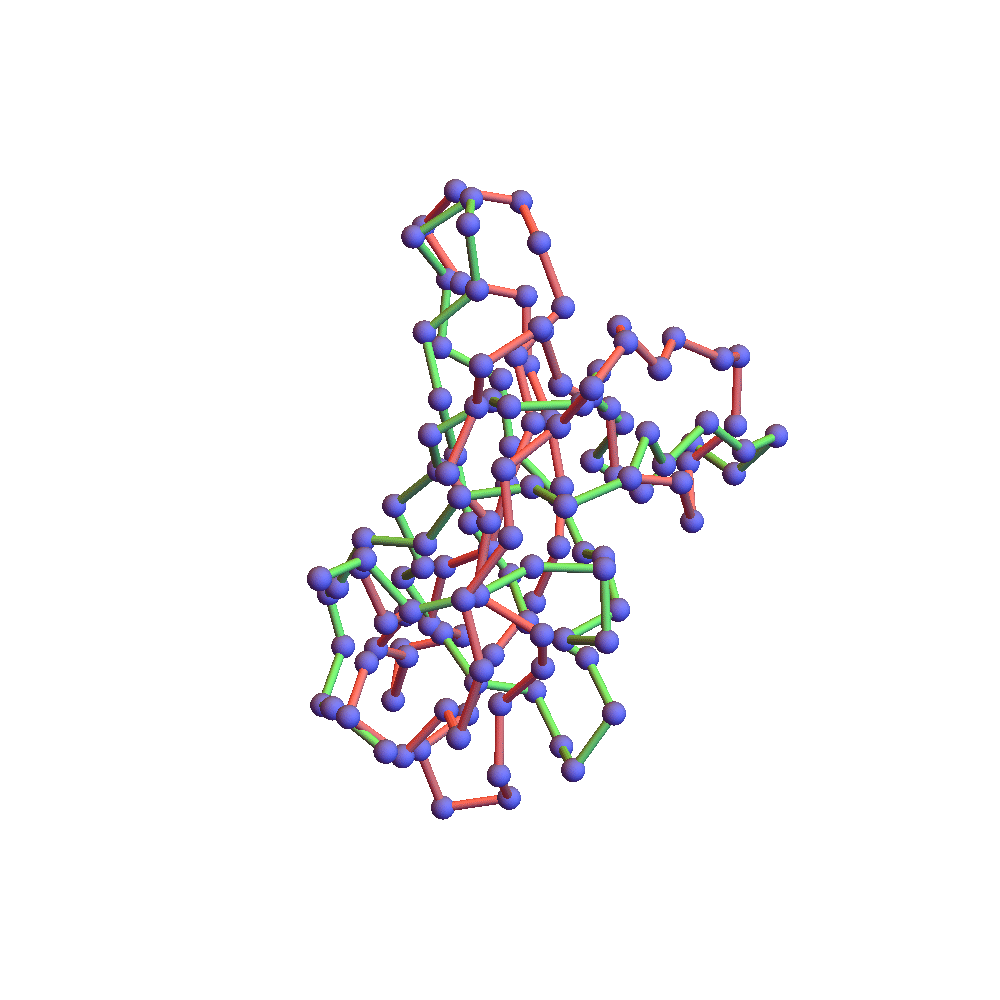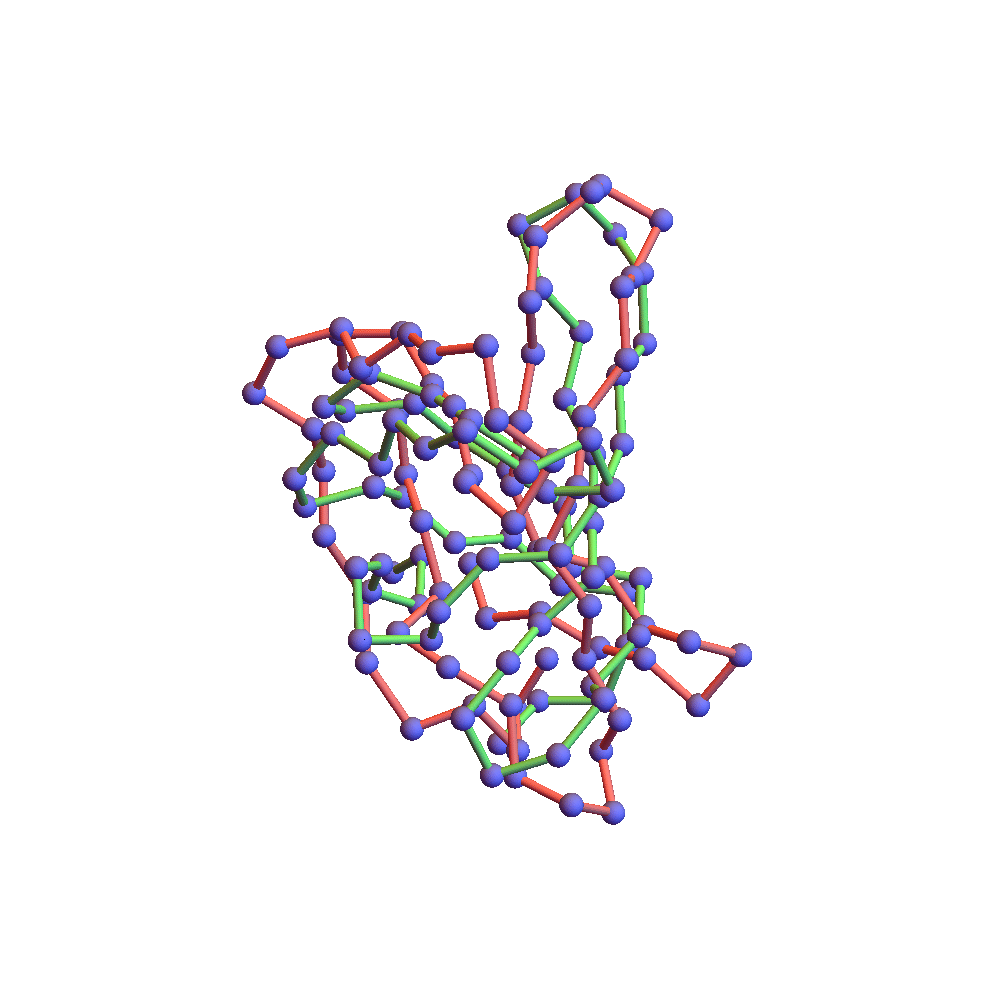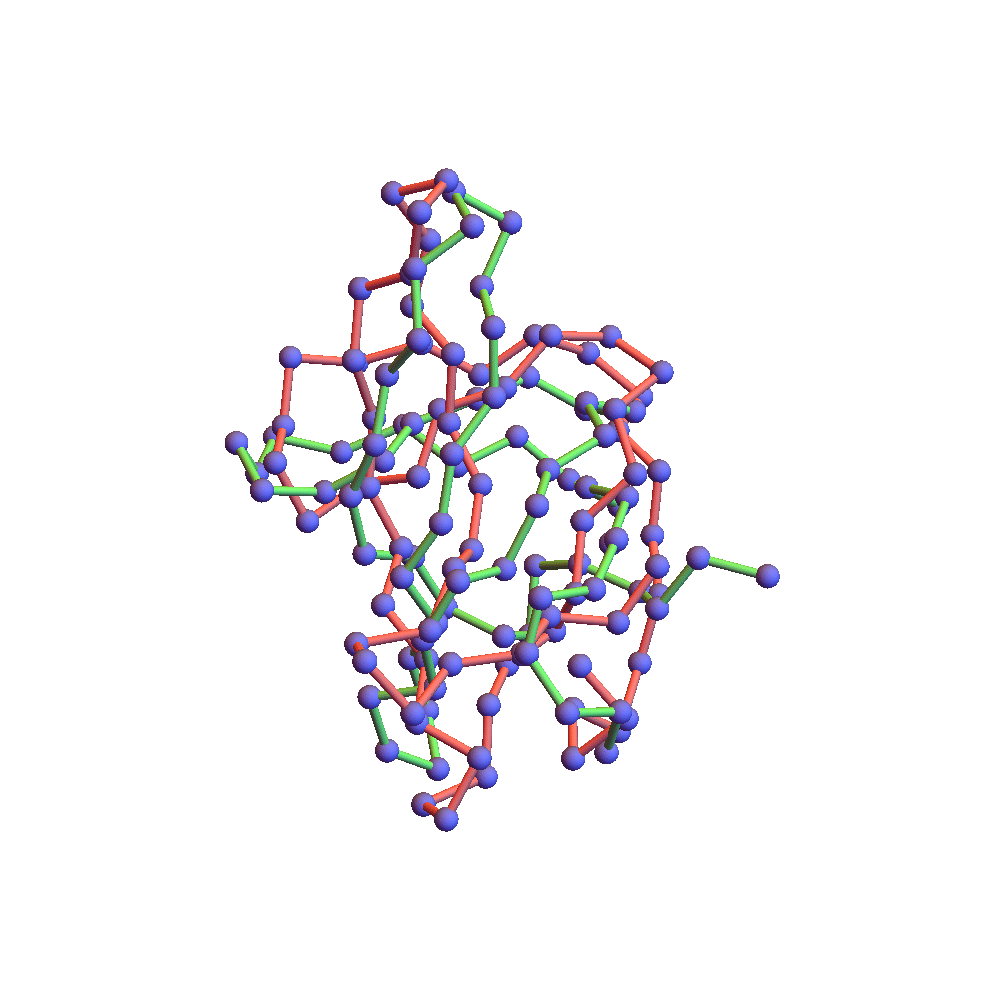
Both runs finished with a discrepancy of 0.09Å, and yet only the top one, with backbone RMSD 1.75Å, I would call a success. I’ve also rendered the results of my 1TG0 folding experiments in the fashion of a CASP competition plot:
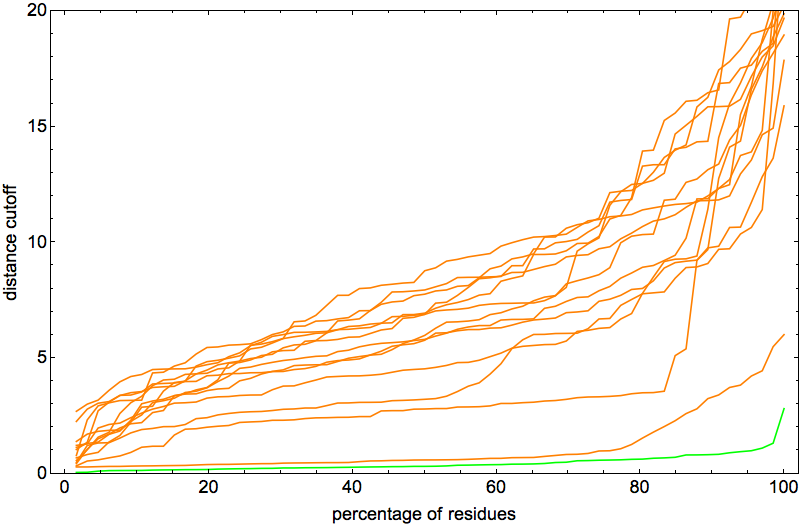
From each of the 14 curves one can read off the percentage of distances (between corresponding α-carbon atoms) below a given cutoff. The lowest of these (not counting the green curve for the native start) is definitely in a class by itself, but litemotifs alone (through the constraint discrepancy) do not set it apart from the rest.
I would like to believe that only a small fraction of proteins are evil (in my technical sense). The next week or two should tell.
