Submitted by ve10 on
Of course I didn’t waste any time this week following up on the idea of using the plentiful solvent oxygen atoms in the PDB to start a library collection of local structures with “solvent contact”. Things developed precisely as I had hoped, and yet by Wednesday I found my thoughts increasingly starting to drift. Turns out there were unresolved questions I had been repressing that finally managed to assert themselves. Fortunately, after some fooling around, by Thursday I’d made a surprising discovery that set me on a somewhat different, and so far the most promising, course.
Tuesday
In close analogy with my definition of backbone contacts, I defined solvent contacts by the property that two side chains, on a given four-residue sequence, make contact with the same solvent-oxygen. Here “make contact” means that some side-chain atom is within 4.5 Å of the solvent atom. I could also have required that the two side-chains make contact with each other, but (after rendering many instances) I found that was usually already the case.
It now seemed that the key statistic was the fraction of backbone atoms, in any one protein, that participate in at least one local structure constraint. I settled on local structures comprising always four contiguous backbone α-carbons, and these making contact either with some other backbone α-carbon or a solvent-oxygen. Here is the histogram for this participation fraction I obtained for a random sample of 100 proteins:
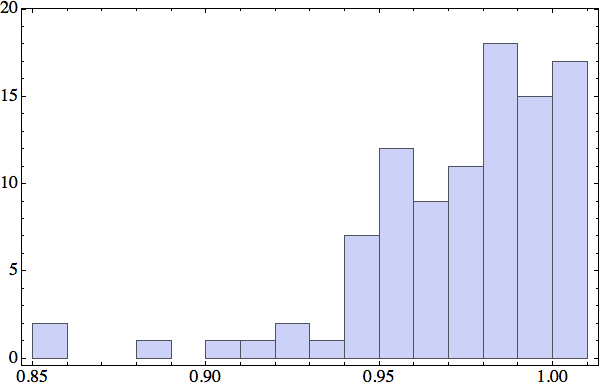
A participation fraction in excess of 95%, for most proteins, showed that the four-backbone-atom scheme could work.
Wednesday
Since Spring Break, you might recall, the plan for invoking any particular local structure as a constraint was to be based on just two of the four (or five) residues, those making the actual contacts. The other two (or three) residue identities were going to be ignored, taking a “wildcard” privilege by virtue of not forming any structurally relevant contacts.
But marking something as not obviously relevant in the constraint geometry is one thing, completely ignoring it is maybe going too far. Chemistry works in strange ways. Even if that middle side-chain, between the two making contacts, does not itself make a contact, surely it makes some difference to the structure if it is, say, small or large, acidic or basic, etc. The more I thought about these wildcard residues, the less I liked the idea of treating them as wildcards!
The wildcard strategy, certainly back when I was thinking in terms of five-backbone-atom local structures, was also meant to address the “call number problem”. There’s no question the PDB is huge, but is it large enough that I will find many hits (and candidate structures) for a random five-residue sequence? By ignoring all except the two relevant residues, or so the proposal, one is guaranteed plenty of hits in the PDB. With four-residue sequences the number of potential call numbers is reduced by about a factor of 20. But is it near the tipping point, where wildcards are no longer necessary?
As an exercise in validating my wildcard strategy, I searched the PDB for hits on a random four-residue sequence: valine (V), glutamic acid (E), isoleucine (I), threonine (T). After all, what chance was there that something as absurd as “VEIT” had evolved and been recorded in the PDB? To my chagrin, this search request yielded 54 hits! Besides the sequence residues, the only other search criterion was my usual X-ray resolution, 1.7 Å. Excited, I immediately downloaded those 54 proteins, extracted the 54 “VEIT” local structures, and was gratified that these all fell into just three types. It appeared that the PDB had the possible structures of “VEIT” completely covered!
Thursday
As already remarked, chemistry works in strange ways, and it is conceivable that one of the least popular four-letter boys names is strangely over-represented in the world of protein residue sequences. In the course of investigating this further, you can imagine the restraint I had to exercise to keep from getting sucked into a trivia vortex. Just a few items of note, for soon-to-be parents. The current champions among girls names are: “LILA” (148 hits), “ELLA” (160 hits). For boys, the leaders are “LARS” (122 hits) and “GAGE” (147 hits).
Sunday
Over Easter weekend I was in Washington DC, visiting my son “TILL” (68 hits), who gave his parents and little brother “TOBY” (sorry, “O” and “B” are not in the residue alphabet) a tour of the Federal Reserve Building. In the early hours at the hotel, while the rest of the family was sleeping, I wrote some code to test the PDB hit rate of four-residue sequences that was scientifically more defensible than sampling internet naming guides.
Using the residue and residue-digram frequencies I extracted from the many proteins on my laptop, I wrote a Markov chain sampler (in Mathematica) for four-residue sequences. My model for the probability of a sequence ABCD is
p(A) p(B) p(C) p(D) c1(A,B) c1(B,C) c1(C,D) c2(A,C) c2(B,D) c3(A,D),
where p is the residue frequency and c1, c2 and c3 are residue pair correlations with separation 1, 2 and 3 on the backbone. The hotel did not have free internet access so I could not query the PDB for hits on my Markov chain generated samples.
Monday
The results of my PDB hit rate experiment are very promising. I’ve summarized things in the following plot:
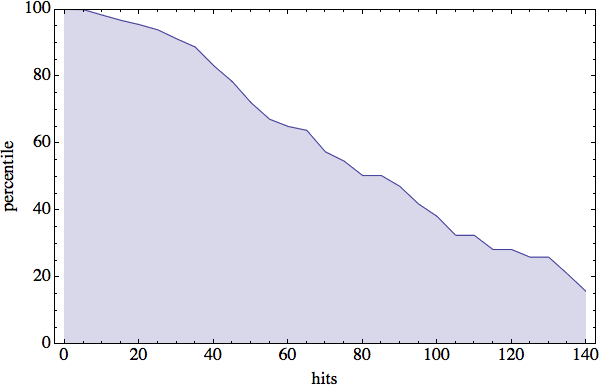
The vertical axis represents percentiles. For example, we see that 50% of all four-residue sequences have 80 or more PDB hits. “ALAS” (199 hits!), it seems that “VEIT” is also slightly unpopular in the protein world. The most significant feature of this plot is the fact that about 90% of all four-residue sequences have at least 30 hits. With that many hits the diversity of structures has a good chance of being covered — but more on that next week.
