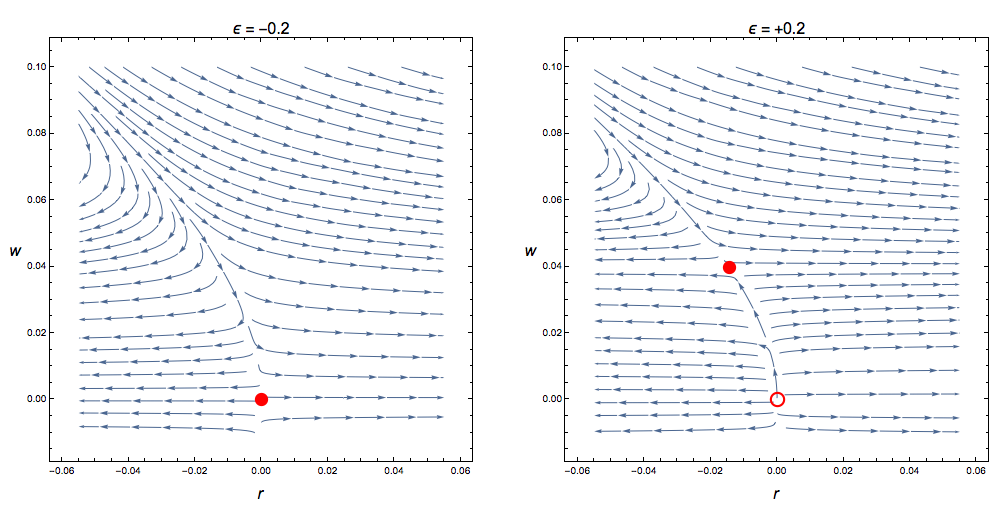
Renormalization group flows, above (left) and below (right) the critical dimension D = 6, for the Potts model in the limit of q = 1. The initial w parameter (of the original model) is large and positive, and flows to the pure quadratic model (w = 0) on long length scales when D > 6. Critical behavior is then determined by the "Gaussian" fixed point (solid red). When D < 6 the downward flow is intercepted by the new "Wilson-Fisher" fixed point (solid red). Notice the Wilson-Fisher fixed point has both stable and unstable axes, just as the Gaussian fixed point for D > 6. The Gaussian fixed point still exists for D < 6 (empty red) but only has unstable axes.
Summary of the renormalization group calculation of percolation exponents
Announcements
- (8/21) The focus of this course is computation, analytical and by machine. Do not take this course unless you have the time to do all the work. There is no required text. Lectures begin August 23.
- (8/25) Here are notes that may clear up confusion about the expected number of solutions of random CNF formulas.
- (8/25) Starting Tuesday, August 30, lecture will be in Rockefeller 110.
- (9/13) Lambert-W (note: the definition used in lecture differs by a minus sign).
- (10/22) Lecture on Tuesday, October 25, is cancelled.
Where & When
- lecture: TR 10:10 - 11:25 am, Rockefeller 110
Contacts
- lecturer: Prof. Veit Elser, email, PSB 426, office hours: Wednesdays 1-3 pm
- grader: Jaron Kent-Dobias, email
Course Content
- satisfiability thresholds, analysis of algorithms
- phase transitions in graphs
- percolation and the Potts model
- scaling and field theory models
- renormalization group
- Markov chains, Monte Carlo
Assignments
- five analytical homeworks
- one computational project
- no exams
Course Grade
80% homework + 20% project
Homework
- (Due 9/1) Use Fourier analysis to compute the electoral vote distribution based on the current polling data. What is the most probable number of votes for Hillary Clinton? Many thanks to Colin Clement for writing a python script for fetching the data!
- (Due 9/15) Assignment 1
- (Due 10/4) Assignment 2
- (Due 10/18) Assignment 3
- (Due 11/1) Assignment 4
- (Due 11/15) Submit a one-page progress report on your computational project. This should include an actual code snippet of the most compute-intensive loop. Use any programming language you wish, as long as it is not a high level and interpreted language such as Mathematica, Matlab, or Python.
- (Due 12/1) Assignment 5
