Submitted by ve10 on
Last week, you may recall, I lamented the fact that my proteins were not dancing. Instead of gracefully exploring conformations, like epileptics in the throes of a tonic seizure, they merely writhed.
You may also recall I had a hypothesis about the catatonic behavior: the imposition of constraints on all parts of the backbone, including loops. Most proteins do not have litemotifs, as I define them, in the poorly packed loop regions. And that’s not a problem, in principle, because even a rather incomplete set of native litemotifs can determine the native fold. The trouble is that for any new residue sequence to be folded, we do not know which litemotifs are native, or which parts of the backbone might be loops and eligible for getting excused from litemotif constraints. In the absence of this knowledge, the folding algorithm was applying litemotif constraints everywhere, even at the truly flexible points along the backbone, the loops!
Also mentioned in the previous post was a simple intervention for the diagnosis/hypothesis of backbone seizure: ignore a given number of litemotif constraints. However, after implementing this in version 3.0 I quickly determined my hypothesis was wrong: the backbones are no less frozen.
I’m now pinning my hopes for fixing the stagnant dynamics by tuning the parameters of the engine at the core of the litemotif-constraint-satisfaction-solver. The engine comprises an iteration scheme wherein projections to constraints of two types are performed and combined. Up to now I’ve used the difference-map scheme, also known as “Douglas-Rachford”, or “project-project-average”. The difference-map has a free dimensionless parameter β, such that the other two algorithms are recovered in the special case β=1. Setting β less than 1 is known to greatly improve the performance of the difference-map in some applications.
The problem with the β parameter in the difference-map is that it doesn’t yet have a satisfactory interpretation. I have therefore lately become a devotee of another iteration scheme, called ADMM, where the role of the parameter is clearer. The Alternating-Direction-Method-of-Multipliers algorithm is widely used in convex optimization. It too has a parameter: α. The special case α = 1 is equivalent to the difference map with β = 1.
To explain the role of α we have to examine the three steps in the ADMM iteration:
y' = PD(z + α x)
z' = PC(y' - α x)
x += z' - y'
As in the formula for the difference map, PD and PC are respectively the “divide” and “concur” projections. There are three sets of variables. The y variables always satisfy the divide constraint: every (divided) copy of the backbone and solvent atoms has the geometry of some litemotif. The concur projection sets all copies equal: these are the z variables. There is another set of variables, x, I’m calling the accumulated discrepancy. We see that, in the third step of the iteration, x is incremented by the difference between the concur and divide variables, the discrepancy. When the discrepancy vanishes, so y' = z', we have a solution-fixed-point (x is then also static because it stops accumulating).
I have implemented ADMM in version 3.0 and find that stagnation is suppressed by setting α to a small value. Here is what I think is going on.
Consider the limit of very small α. In this limit the x variables play almost no role, and the iteration reduces to the naive scheme of alternating projections. Alternating projections is hopeless for hard problems because of the very many instances of mutually proximal pairs of points on the two constraint sets: the algorithm quickly finds such pairs and then cannot escape from them. In ADMM the discrepancy y' - z' is accumulated in x, and after it has grown sufficiently large, there is enough of a shift in the arguments of the two projections to escape the trap.
What I believe is peculiar to the folding application is that the ADMM discrepancy has trouble accumulating unless α is quite small. The argument goes like this:
By the nature of the litemotif constraints on the backbone, the convergence to an alternating-projections fixed point (α = 0) is quite slow. That’s because the constraints along the backbone are for the most part local. In each (alternating projection) iteration, information moves a fixed unit along the backbone; bringing the entire backbone into alternating-projections equilibrium thus requires a number of iterations that scales with the length of the backbone. And since it is the alternating-projections fixed point that determines the discrepancy, many iterations are needed before a reliable discrepancy is even established. By keeping α very small, we allow enough time for the discrepancy to converge and convey global information to the two constraint projections.
The two movies below show the protein 2P5K being folded by ADMM with two settings for α: 1.0 (top) and 0.05 (bottom). Each shows 20 frames taken at 1,000 iteration intervals. I’m now rendering solvent as white spheres. The red tint on the bonds of the backbone convey the distance of the best litemotif (for the two atoms joined by the bond and their neighbors on the backbone). In both runs I dropped litemotif constraints at four points along the backbone (the four reddest).
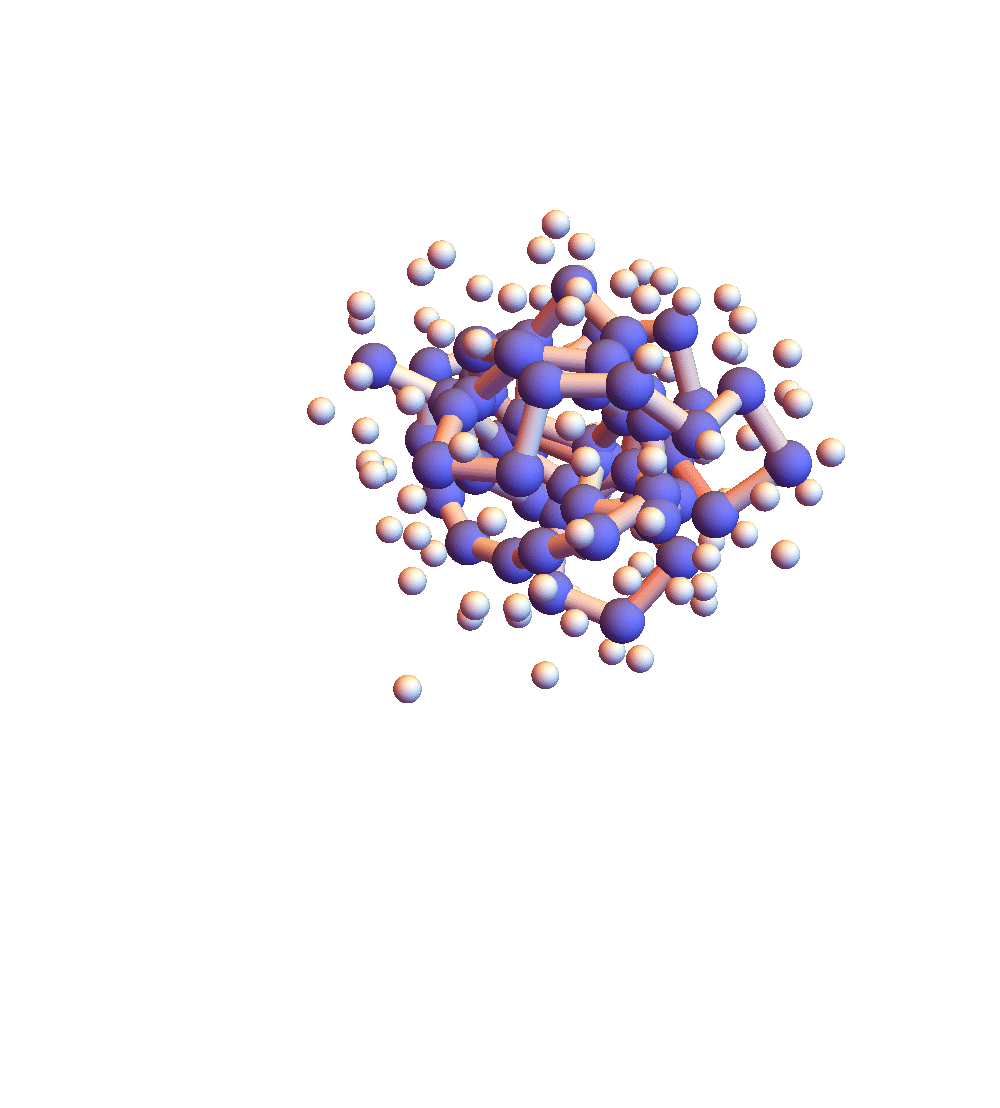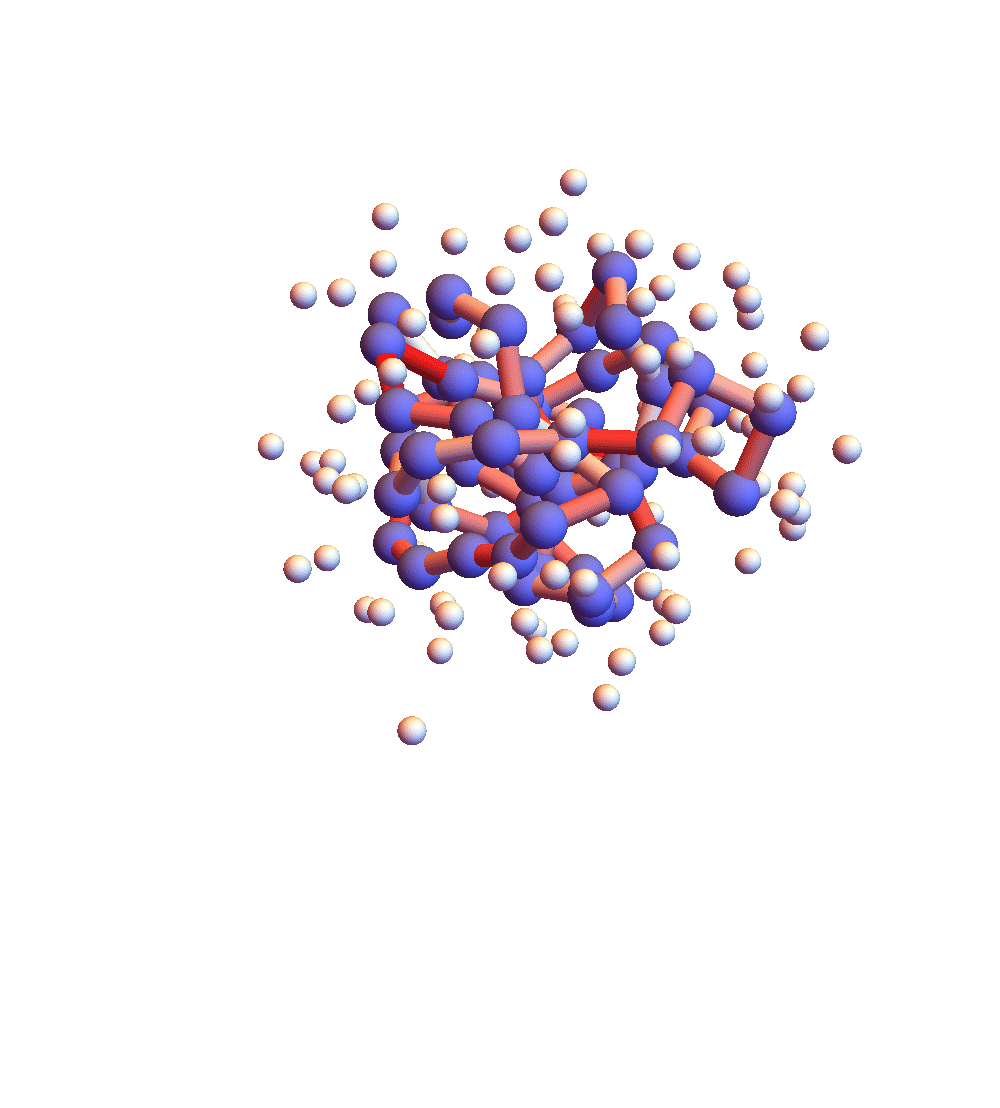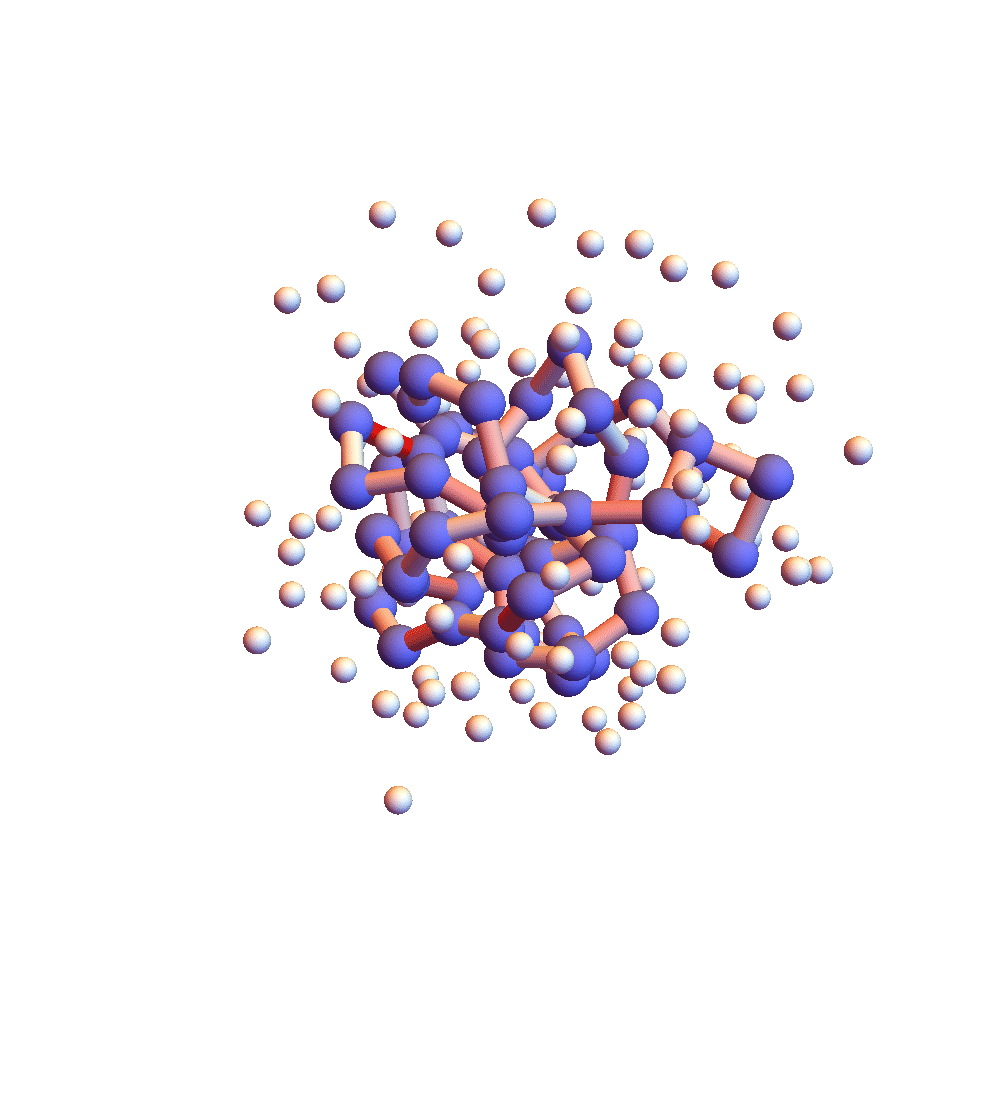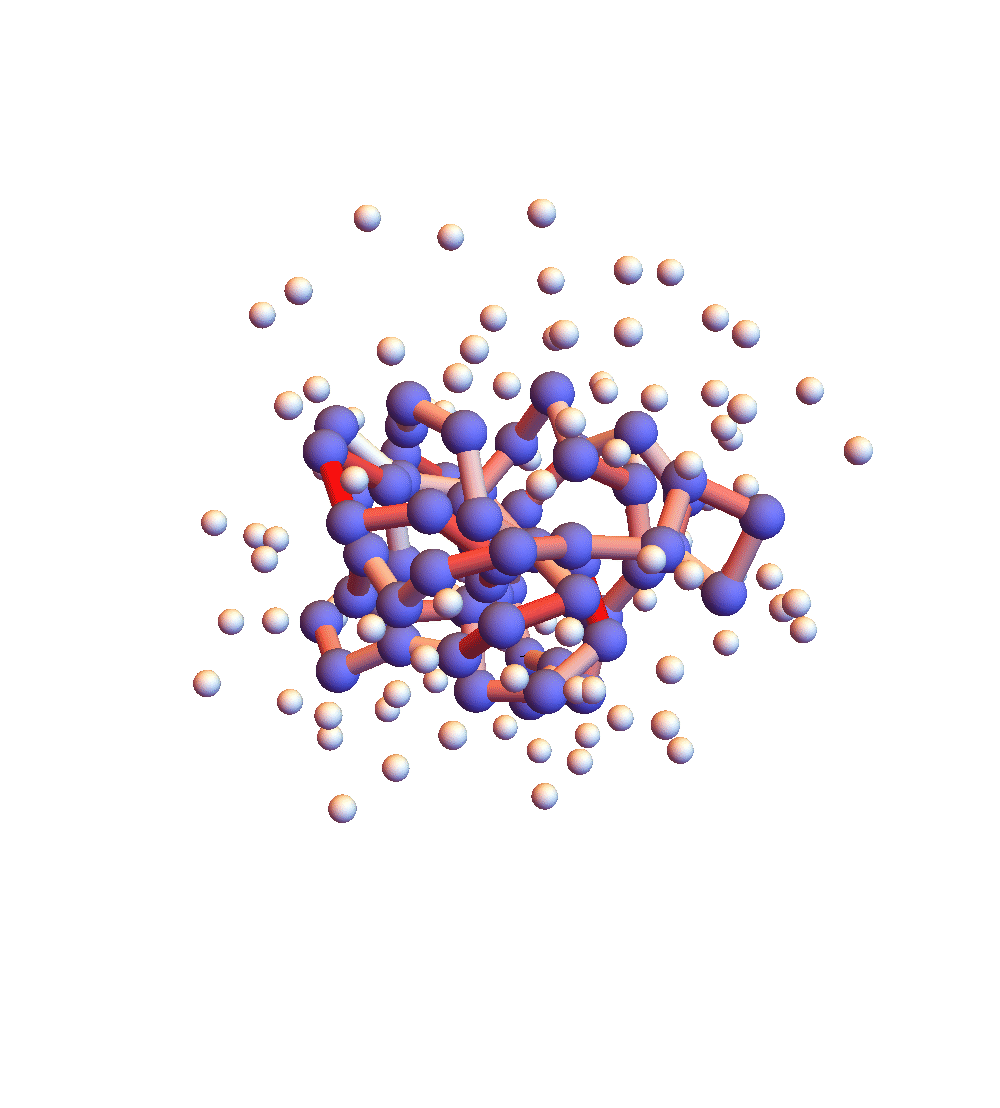
 It has probably not escaped your notice that these proteins settle into a state of uniform motion, a response to an accumulated discrepancy that surely is spurious. Fixing that will be first on my list for next week.
It has probably not escaped your notice that these proteins settle into a state of uniform motion, a response to an accumulated discrepancy that surely is spurious. Fixing that will be first on my list for next week.
