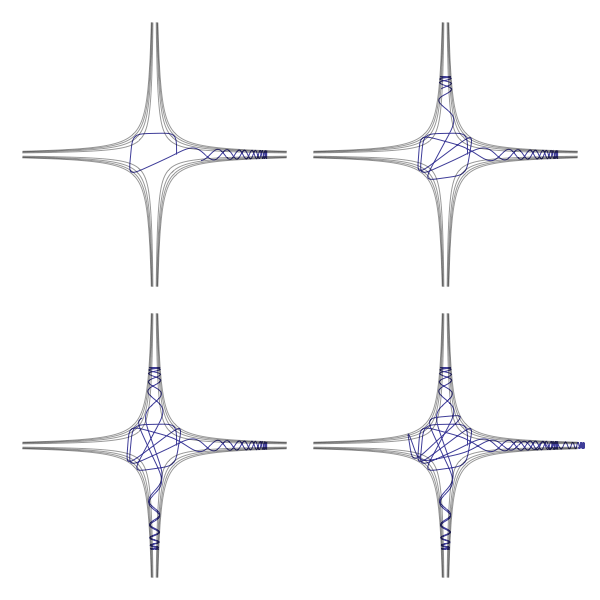
Above are trajectories traced out after 1, 2, 3 and 4 seconds of a particle moving in the plane subject to a potential energy V(x,y) = x²y² (contours in black). As the particle enters one of the four "canyons", its motion along the canyon axis is increasingly converted to transverse oscillatory motion until it is reflected back to the origin. Since the phase of the oscillatory motion is quite random when the particle emerges at the origin, so will be the selection of the next canyon it enters.

This system, for which the "mixing" mechanism responsible for chaos is particularly transparent, is a special case of the field-amplitude dynamics in a generalization of Maxwell's equations known as quantum-chromo-dynamics, or QCD. The x and y components of the particle position correspond to the x and y components of the QCD vector potential, which in this chaotic motion have different "colors". 

          Announcements

• (5/16) I will be away from my office until 2 PM today, and all of the weekend, but will be regularly checking my email and welcome your questions about Hamiltonian dynamics, the two-body problem, etc.
• (5/13) Here is the final exam. Please read the instructions on the cover page first.
• (5/12) Graded homework assignments (11 and 12) can be picked up outside Prof. Elser's office, 426 PSB.
• (5/4) The final exam is take-home and covers just the last third of the course: Hamiltonian dynamics (mostly) and the two-body problem. The format will be similar to the prelims and the same rules (no electronic aids, written sources) apply. You may spend up to six hours on the exam, split up into at most two sessions. The exam is designed to work as a standard 2.5-hour final, so the time limits are very generous. Print out the exam after it is posted May 13 on this webpage. It is due in the Physics Department office no later than May 20.
• (5/2) Here are a couple of things to be thinking about as you watch the Levitron movie. The adiabatic invariant I in this system is the projection of the top's spin angular momentum onto the axis defined by the local direction of the magnetic field in which it moves. The quantum analog of I is the quantized z-component of spin angular momentum (with z aligned with the magnetic field), also having units of action. Combining the magnetic-dipole energy of the top with its gravitational potential energy, the top's net potential energy is U = -μ I B(x,y,z) + m g z, where B is the magnitude of the magnetic field. The Levitron base magnet is designed so that U has a stable minimum in which the top can dance around. For adiabatic invariance to hold, the dancing motion of the center of mass must be slow compared to the fast periodic motion of the top's precessing axis. If you look closely, you will see that this is true up until the point when the top flips over.
• (3/5) We are back on our original homework schedule,  assignments are due Wednesdays. This week we have a grace period, until Friday, for those who didn't check the due date on the assignment. 
• (2/27) Homework assignment 5 has been updated, so be sure to download the current version.
• (2/27) Here is the formula sheet you will have on the prelim. Do not jump to the conclusion that you will be needing all of these formulas, because the exam cannot nearly cover all this material.
• (2/24) The prelim Friday only covers rotating frames and rigid body motion. Here is the prelim from last year, if you're curious about length and style and not content.
• (2/19) No homework assignment this week. Use your 3318 study time preparing for the Feb. 28 prelim.
• (2/10) Welcome to the Physics 3318 website!

Where & When

• Lecture: MWF 10:10 - 11:00 am, Rockefeller 102
• Discussion: T 2:30 - 3:20 pm, Clark 294D
• Study Group: Th 1:15 - 3:15 pm, Clark 294C

Contacts

• lecturer: Prof. Veit Elser, email, office hours: Th 2:15 - 3:15 pm, Clark 294C
• discussion leader: Riccardo Pavesi, email, office hours: Th 1:15 - 2:15 pm, Clark 294C
• grader: Ismail El Baggari , email

Course Content

• Rotating frames, rigid body motion
• Lagrangian formalism
• Variational principles, constraints
• Action principle, quantum mechanics
• Central force problem
• Hamiltonian formalism
• Adiabatic principle, more quantum mechanics

Exams

• prelim 1: February 28 (in class)
• prelim 2: April 11 (in class)
• final: May 20, 2 pm

Course Grade

35% homework + 20% prelim 1 + 20% prelim 2 + 25% final